Решите номер 5 .Есть вложение. 25 б . С исследованием пожалуйста.

Question

Дан 1 ответ

Правильный ответ

$y=(-2)^5*\sqrt{|x^2-3|^4}$

Т.к. модуль возводиться в чётную степень, от него можно избиваться.

$y=(-2)^5*\sqrt{(x^2-3)^4}\\y=(-2)^5*(x^2-3)^2$

1. Область определения все числа.

2. От х берётся чётная степень, поэтому функция чётная (со словами просто совпадение), то есть y(x)=y(-x), таким образом можно построить график функции справа и отразить его на лево.

3. Найдём точки пересечения с осями:

x^2-3=0=>x=б\sqrt{3}" alt="y(0)=(-2)^5*(0^2-3)^2=-32*9=-288\\0=(-2)^5*(x^2-3)^2=>x^2-3=0=>x=б\sqrt{3}" align="absmiddle" class="latex-formula">

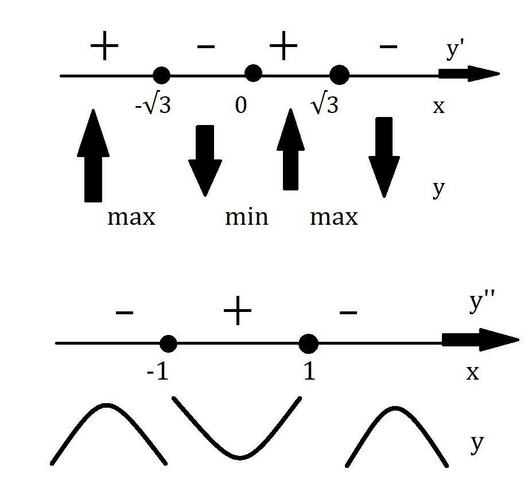
4. Исследование с помощью первой производной (экстремумы и возрастания и убывание функции).

$y'=-2(x^2-3)(2x)=-4x(x+\sqrt{3} )(x-\sqrt{3} )$

Cм. внизу

5. Исследование с помощью второй производной (точки перегиба, выпуклости и вогнутости).

$y'=-4x^3+12x\\y''=-12x^2+12=-12(x-1)(x+1)$

См. внизу

6. Исследование на асимптоты:

$\lim_{x \to \infty }{(kx+b-f(x))}$

Формула чтобы найти уравнение асимптоты. Найдём k.

$\lim_{x\to\infty }{\frac{f(x)}{x}}\\\lim_{x \to\infty }{\frac{(-2)^{5}(x^{2}-3)^{2}}{x}}=\\\lim_{x\to\infty }{\frac{-32*x^{4}+192*x^{2}-288}{x}} = -\infty$

Т.к. коэффициент равен -∞, то асимптот не существует.

WhatYouNeed_zn (34.7k баллов) 01 Июнь, 20