Найдите площадь фигуры ограниченной линиями y=x^2+1, y=0,x=-2, x=2

Чтобы решить эту задачу надо понимать, что такое интеграл.

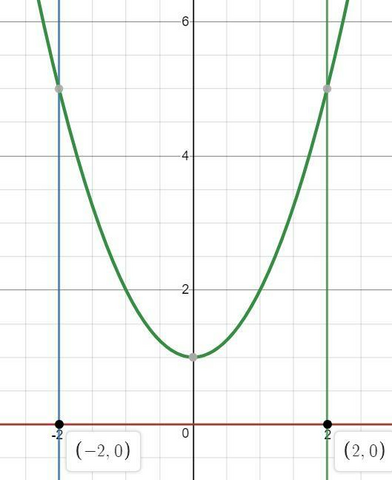
Нам всего лишь необходимо найти площадь под графиков функции y=x^2+1, от -2 до 2.

$S=\int\limits^2_-2 {x^2+1} \, dx =F(x)|^2_{-2}\\F(x)=\frac{x^3}{3} +x\\S=F(2)-F(-2)=\frac{8}{3} +2-(\frac{-8}{3} -2)=\\=16/3+4=9+1/3$

Хотя вообще функция симметрична оси у и можно было просто умножить на 2, площадь под графиком у=х^2+1, от 0 до 2.

Ответ: S=9+1/3