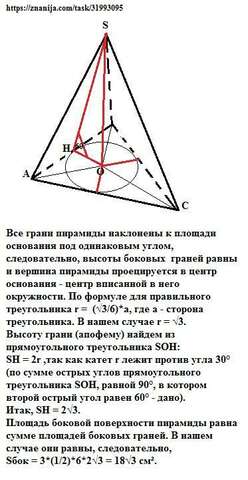
Все грани пирамиды наклонены к площади основания под одинаковым углом, следовательно, высоты боковых граней равны и вершина пирамиды проецируется в центр основания - центр вписанной в него окружности. Пирамида правильная.
По формуле для правильного треугольника r = (√3/6)*a, где а - сторона треугольника. В нашем случае r = √3.
Высоту грани (апофему) найдем из прямоугольного треугольника SOH:
SH = 2r ,так как катет r лежит против угла 30° (по сумме острых углов прямоугольного треугольника SOH, равной 90°, в котором второй острый угол равен 60° - дано).
Итак, SH = 2√3.
Площадь боковой поверхности пирамиды равна сумме площадей боковых граней. В нашем случае они равны, следовательно,
Sбок = 3*(1/2)*6*2√3 = 18√3 см².