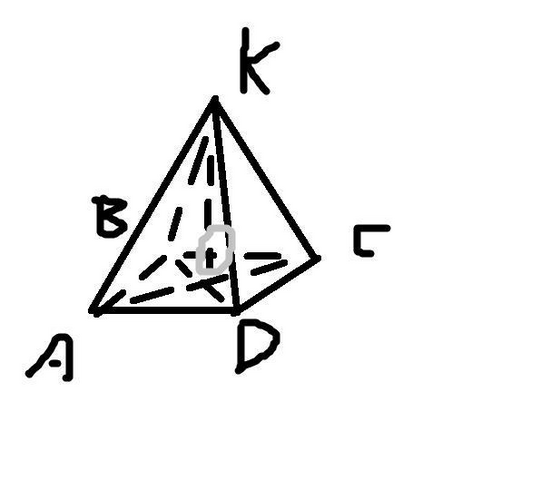
Исходя из рисунка AK=BK=CK=DK = 6 см, OK = 4 см. По теореме Пифагора BO=AO=CO=DO=√(36см²-16см²)=2√5см, тогда по теореме Пифагора AB=BC=CD=AD=√(20см²+20см²)=2√10см, тогда Sквадрата = 2√10см*2√10см = 4*10см²=40см². ПУсть KH - высота к DC, тогда DH=HC = DC / 2 = 2√10см/2 = √10см, тогда по теореме Пифагора KH = √(36см²-10см²)=√26см, тогда площадь каждого из четырех боковых треугольников равна 1/2*√26см*2√10см=2√65см², тогда Sпов. = Sквадрата+4*Sбок.треугольника = (40+4*2√65)см²=8*(5+√65)см²
Ответ: 8*(5+√65)см²