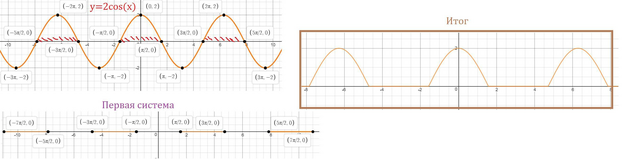
Раскроем модуль по определению
![\left[\begin{array}{cc}\left \{ {{\cos{x}<0} \atop {y=\cos{x}-\cos{x}} \right. \\\left \{ {{\cos{x}\geq 0} \atop {y=2\cos{x}}} \right. \end{array}\right]](https://tex.z-dn.net/?f=%5Cleft%5B%5Cbegin%7Barray%7D%7Bcc%7D%5Cleft%20%5C%7B%20%7B%7B%5Ccos%7Bx%7D%3C0%7D%20%5Catop%20%7By%3D%5Ccos%7Bx%7D-%5Ccos%7Bx%7D%7D%20%5Cright.%20%5C%5C%5Cleft%20%5C%7B%20%7B%7B%5Ccos%7Bx%7D%5Cgeq%200%7D%20%5Catop%20%7By%3D2%5Ccos%7Bx%7D%7D%7D%20%5Cright.%20%5Cend%7Barray%7D%5Cright%5D "\left[\begin{array}{cc}\left \{ {{\cos{x}<0} \atop {y=\cos{x}-\cos{x}} \right. \\\left \{ {{\cos{x}\geq 0} \atop {y=2\cos{x}}} \right. \end{array}\right]")
Первая система "говорит", что когда х∈( π/2+2π*n ; 3π/2+2π*2 ), n∈Z.
То y=0
Вторая система "говорит", что когда х∈[ -π/2+2π*k ; π/2+2π*k ], k∈Z.
То y=2cos(x), Построим эту функцию и выделим значение, которые принадлежат этим промежуткам х. Найдём наибольшее значение y(2π*l)=2*1=2, l∈Z. Найдём наименьшее значение y(-π+2π*l)=2*-1=-2, l∈Z.
Найдём корни 0=2cos(x) --> x={±π/2+2π*t}, t∈Z. Смотри вниз. Как видно эти корни совпадают в ограничением второй системы, то есть всё что выше или принадлежит оси Оу, то нам подходит. Ну а дальше объединяем первую и вторую систему.
