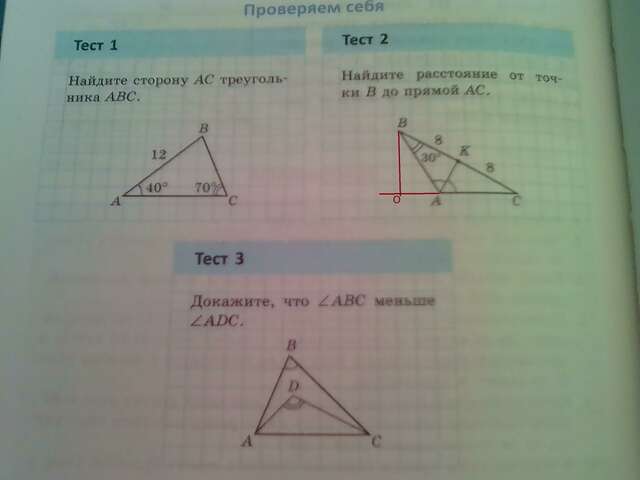
1) В Δ ABC ∠B = 180°-70°-40° = 70°. Треугольник равнобедренный, так как углы при основании BC равны. ⇒ Боковые стороны равны. AB = AC = 12/
2) Расстоянием от точки до прямой является длина перпендикуляра, опущенного из точки на прямую. Опустим из тч.B перпендикуляр BO на прямую AC.
по чертежу: так как AK является медианой (делит противолежащую сторону пополам) и биссектрисой (делит угол A на два равных угла), то ΔABC равнобедренный и угол при вершине C = 30°.
В ΔOBC ∠O = 90°, ∠C = 30° ⇒ OB является катетом, лежащим против угла 30° и он равен половине гипотенузы BC. OB = 8. Расстояние от точки В до прямой AC равно 8.
3) В Δ ABC ∠ABC + ∠BAC + ∠ACB = 180°.
В Δ ADC ∠ADC + ∠DAC + ∠ACD = 180°.
Но ∠DAC меньше ∠BAC (так как ∠DAC является частью ∠BAC), и ∠ACD меньше ∠ACB (так как ∠ACD является частью ∠ACB).
Так как суммы углов = 180°, то ∠ADC больше ∠ABC.