1. Постройте график функции y=x^2+4x+3Найдите:А) наимененьшее значение функцииБ) значение...

Question

1. Постройте график функции y=x^2+4x+3Найдите:А) наимененьшее значение функцииБ) значение x, при которых значение функции равно 8В) значение x, при которых функция принимает положительные значения; отрицательные значения.Г) промежутки, на которых функция возрастает; убывает.2. Найдите координаты вершины параболы y= -(x+1)^2 - 4. Постройте этот график

Answer 1

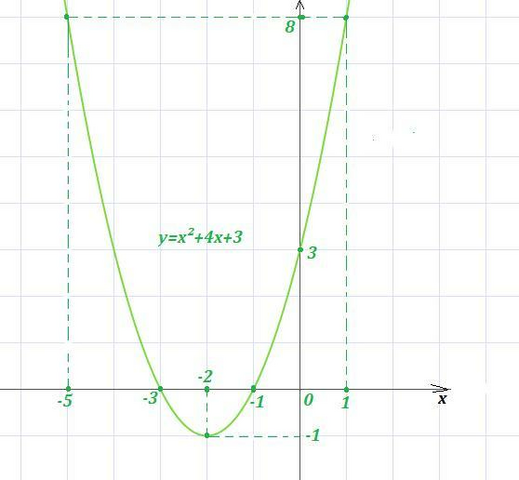
0\; \; \; \to \; \; \; x\n (-\infty ,-3)\cup (-1,+\infty )\\\\x^2+4x+3<0\; \; \; \to \; \; \; x\in (-3,-1)\\\\d)\; \; y(x)\; vozrastaet:\; \; x\in (-2,+\infty )" alt="1)\; \; y=x^2+4x+3\\\\a)\; \; x_{versh}=-\frac{b}{2a}=-\frac{4}{2}=-2\\\\y_{naimen}=y_{versh}=(-2)^2-4\cdot 2+3=-1\\\\b)\; \; x^2+4x+3=8\; \; \to \; \; x^2+4x-5=0\; \; ,\; \; x_1=-5\; ,\; \; x_2=1\\\\y(-5)=8\; ,\; \; y(1)=8\\\\c)\; \; x^2+4x+3=0\; \; \Rightarrow \; \; \; x_1=-3\; ,\; x_2=-1\; \; (teotema\; Vieta)\\\\znaki:\; \; \; \; +++(-3)---(-1)+++\\\\x^2+4x+3>0\; \; \; \to \; \; \; x\n (-\infty ,-3)\cup (-1,+\infty )\\\\x^2+4x+3<0\; \; \; \to \; \; \; x\in (-3,-1)\\\\d)\; \; y(x)\; vozrastaet:\; \; x\in (-2,+\infty )" align="absmiddle" class="latex-formula">

---