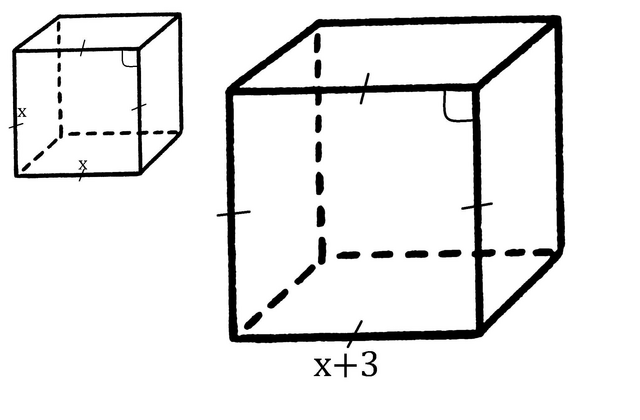
Куб имеет 6 граней, каждая из которых является квадратом со стороной, равной ребру куба.
Пусть ребро куба равно x. Тогда площадь его поверхности 6·х².
После увеличения ребра на 3, его длина равна x+3, а площадь поверхности куба: 6·(x+3)².
По условию:
6x² + 162 = 6(x+3)² = 6(x²+6x+9)
0 = 6x²+36x+54 - 6x² - 162
36x-108 = 0
36x = 108
x = 108:36 = 3
Ответ: 3.