Отрезок AB является диаметром окружности с центром в точке О. Точка М лежит **...

Question

Отрезок AB является диаметром окружности с центром в точке О. Точка М лежит на окружности, при этом угол MAB=40 а) Определите углы треугольника MOB б) Среди дуг AM, MB, AB укажите наибольшую и наименьшую в) Какие из отрезков с концами в точках M, A, B, O перпендикулярны? 8 класс Пожалуйста с решениями, очень нужно

Answer 1

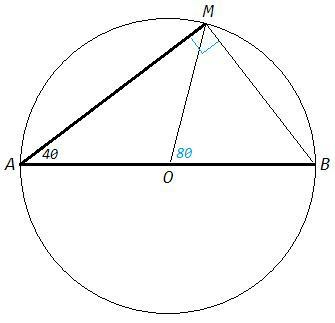
а) Вписанный угол равен половине центрального, опирающегося на ту же дугу. ∠MAB - вписанный, ∠MOB - центральный, оба опираются на дугу MB.

∠MOB=2∠MAB =40° *2 =80°

∠MOB - равнобедренный (OM=OB, радиусы)

∠OMB=∠OBM =(180°-∠MOB)/2 =50°

б) Угловая величина дуги равна опирающемуся на неё центральному углу.

∪MB=∠MOB =80°

∪AB=∠AOB =180° (∠AOB - развернутый угол. Диаметр делит окружность на две равные дуги.)

∪AM=∪AB-∪MB =180°-80° =100°

∪MB < ∪AM < ∪AB

в) Вписанный угол равен половине дуги, на которую опирается. Вписанный угол AMB опирается на диаметр AB, а значит на дугу 180°.

∠AMB=180°/2 =90° (Вписанный угол, опирающийся на диаметр - прямой)

AM⊥MB

---