1. Найдем производную данной функции
f ` (x) = 3x² - 6x - 9 = 3(x² - 2x - 3)
2. Приравняем к нулю производную и найдем точки экстремума.
f ` (x) = 0 ⇒ x² - 2x -3 = 0 ⇒ (x-3)(x+1) = 0
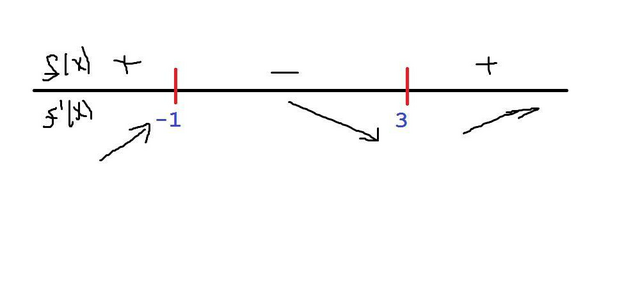
3. Строим числовую прямую, отмечаем точки 3 и -1 ( на рисунке)
Замечаем, что точка максимума функции это -1, а точка минимума это 3
Функция возрастает на промежутке ( - ∞; -1] V [3 ; +∞)
Функция убывает на промежутке от [-1; 3]