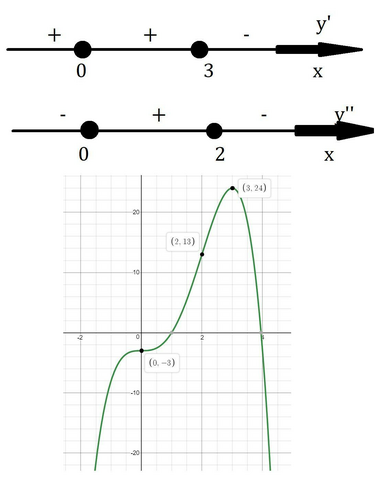
Как видно производная обращается в ноль при x=3 и x=0 это критические точки, используем метод интервалов, для определения знака производной на промежутках.
При x=0, производная не меняет знак, значит это не экстремум функции. При x=3, производная меняет знак с плюса на минус, значит это минимум функции.

На (-∞;0)∪(0;3) функция растёт.
На (3;+∞) функция убывает.
Функция общего вида (не обладает чётность или нечётностью)
Найдём точки перегиба функции.

x=0 и x=2 это точки перегиба.
На (-∞;0)∪(2;+∞) функция выпукла вверх.
На (0;2) функция выпукла вниз.
Найдём координаты всего чего ещё не нашли.

Можем строить.
Наименьшее значение (-∞;-∞) и (+∞;-∞)
Наибольшее значение (3;24)