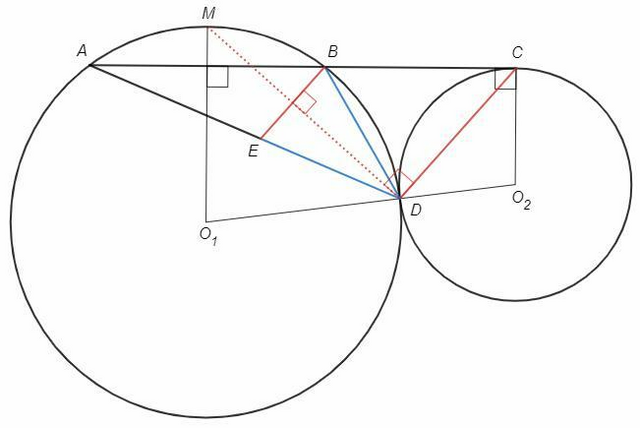
DM - биссектриса угла ADB, M - середина дуги AB.
O1M⊥AB (радиус, проведенный через середину дуги)
O2C⊥AC (радиус, проведенный в точку касания)
O1M||O2C => MO1D+CO2D=180 (внутренние односторонние углы)
△MO1D, △CO2D - равнобедренные
2 MDO1 +2 CDO2 =180 <=> MDO1+CDO2=90 => MDC=90
ED=BD, △BDE - равнобедренный
DM - биссектриса и высота
DM⊥BE, DM⊥CD => BE||CD
AB/AE=AC/AD (теорема о пропорциональных отрезках)
BC/AC=ED/AD => BC/AC=BD/AD
AB=BC, BD/AD=BC/AC=1/2 => AD=7*2=14