В параллелограмме АВСД через точку пересечения диагоналей проведена прямая, которая...

Question

В параллелограмме АВСД через точку пересечения диагоналей проведена прямая, которая отсекает на сторонах ВС и АД отрезки ВЕ = 1,6 и АК = 6,4. Точка М – точка пересечения прямых АВ и ЕК. Найдите периметр и площадь треугольника АВД, если ВМ = 1, а величина угла ВАД 60°.

Answer 1

Ответ:

P = 22 ед.  S = 12√3 ед².

Объяснение:

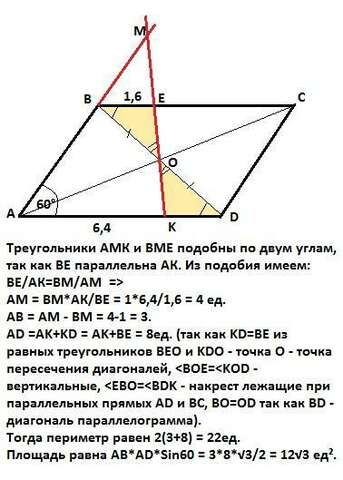
Треугольники АМК и ВМЕ подобны по двум углам, так как ВЕ параллельна АК. Из подобия имеем:

ВЕ/АК=ВМ/АМ  => AM = ВМ*АК/ВЕ = 1*6,4/1,6 = 4 ед.

АВ = АМ - ВМ = 4-1 = 3.

AD =AK+KD = AK+BE = 8ед. (так как KD=ВЕ из равных треугольников ВЕО и KDO - точка О - точка пересечения диагоналей).

Тогда периметр равен 2(3+8) = 22ед.

Площадь равна АВ*AD*Sin60 = 3*8*√3/2 = 12√3 ед².

---