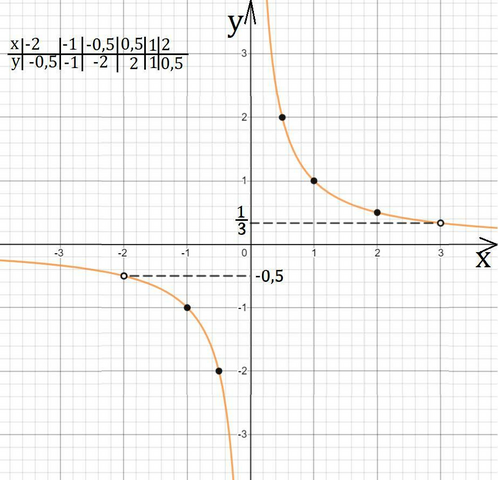
это функция обратной пропорциональности
это функция обратной пропорциональности  , графиком будет гипербола ветви которой симметричны относительно начала координат и расположены в 1 и 3 четвертях т.к. t=1>0.
, графиком будет гипербола ветви которой симметричны относительно начала координат и расположены в 1 и 3 четвертях т.к. t=1>0.
Раз x≠{-2;3}, то у гиперболы будут выколоты точки (-2;-0,5), (3;1/3).
Таблицу точек для построения и график смотри внизу.
Прямая y=kx, так же симметрична относительно начала координат, поэтому прямая будет имеет только одну общею точку с графиком, когда она проходит через одну выколотую точку. По координатам выколотых точек, можно заметить что они не симметричны относительно (0;0), поэтому прямая y=kx не может проходить через них одновременно. Найдём k.


Ответ: 1/9 и 0,25.