Ответ:
Объяснение:
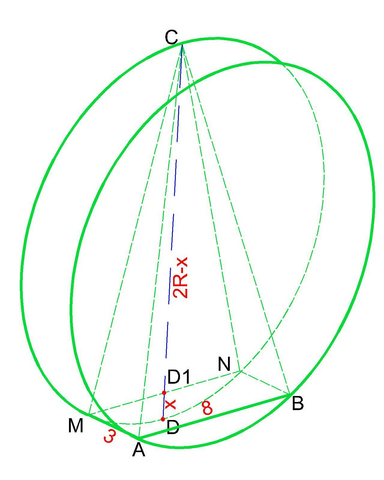
А) докажем что АВNM - прямоугольник.
Имеем 2 параллельные плоскости - основания цилиндра. Плоскость, проходящая через хорду АВ перпендикулярна прямой CD, лежащей в плоскости основания. Значит плоскость сечения перпендикулярна плоскостям основаниий цилиндра, а т.к. цилиндр прямой, то и высоты цилиндра AM и BN, образованные сечением ABNM перепендикулярны плоскостям оснований. В результате получаем четырёхугольное сечение, все внутренние углы которого прямые. Это - прямоугольник.
Диагонали прямоугольника равны!
Б) Найдём объём пирамиды CABNM.
Формула вычисления объёма пирамиды
V=1/3·S·h, где S-площадь основания, h-высота пирамиды.
Очевидно, что S=8*3=24.
Найдём h=CD₁.
Используем свойство хорд: если 2 хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
В нашем случае хордами выступают MN=AB=R и CD=2R.
Хорда MN делится на MD₁=ND₁, т.к. хорда CD является диаметром и пересекает хорду MN под прямым углом, разделяя её пополам.
Составим уравнение, обозначив за х D₁D - меньшую часть хорды CD отсеченную плоскостью ABNM:
x·(2R-x) =0.25R²
Для удобства дальнейших расчетов подствим вместо R числовое значение:
х·(16-х)=16
х²-16х+16=0
D=16²-4*16=192
x₁=(16+√192)/2=8+4√3
x₂=(16-√192)/2=8-4√3
Здесь решение x₁ - это случай, когда точка D и центр основания лежат по одну сторону от плоскости сечения (т.к. в нашем случае там находится точка С, то это и есть высота пирамиды,
а х₂ - это отрезок DD₁ изначально принятый за х.
Значит DD₁=8-4√3 и проверим высоту пирамиды
h=CD₁=(2R-x)=16-8+4√3=8+4√3 (совпало с х₁) - это можно выпустить. Простая проверка.
V=1/3·S·h=1/3·24·(8+4√3)=64+32√3 кубических единиц.