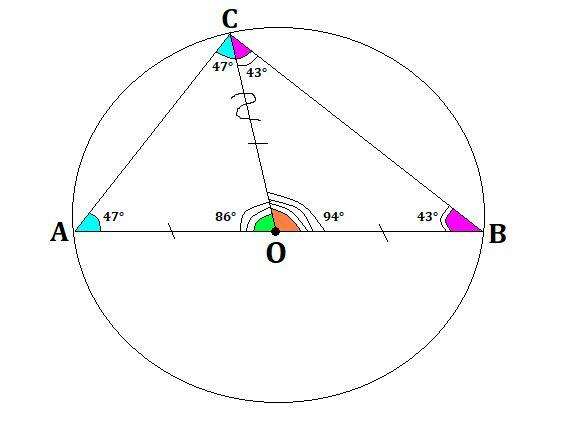
Решение:
Так как OC и AO - радиусы окружности с центром в точке O ⇒ AO=OC (точки на окружности равноудалены от центра).
Поскольку AO=OC ⇒ ΔAOC - равнобедренный.
∠CAO=∠ACO=47° (по свойству равнобедренного треугольника).
Сумма углов треугольника равна 180°.
⇒ ∠AOC=180°-(47°+47°)=180°-94°=86°.
Сумма смежных углов равна 180°.
∠AOC смежный с ∠COB ⇒ ∠COB=180°-86°=94°.
Так как CO и OB - радиусы окружности с центром в точке O ⇒ CO=OB (точки на окружности равноудалены от центра).
Поскольку CO=OB ⇒ ΔCOB - равнобедренный.
∠OCB=∠CBO (по свойству равнобедренного треугольника) ⇒ их сумма равна 180°-94°=86°, а каждый из них по 43°.
Также можно было найти ∠OCB и ∠CBO по-другому:
Вписанный угол, который опирается на полуокружность, равен 90°.
∠ACB=90°, так как он вписанный (он же ∠С).
Поскольку ∠ACO=47° ⇒ ∠OCB=90°-47°=43°.
Так как ΔCOB - равнобедренный ⇒ ∠OCB=∠CBO (он же ∠B) =43° (по свойству равнобедренного треугольника).
Ответ: 43°; 90°.