На оси ординат Найдите точку равноудаленную от точек е(1;2) f (3;4)

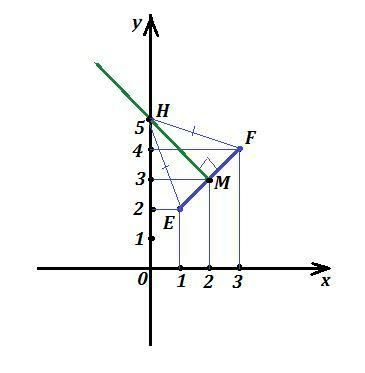
Точка, равноудалённая от двух других точек ( Е и F ) лежит на серединном перпендикуляре. Составим уравнение прямой EF.

$E(1,2)\; ,\; \; F(3,4)\\\\y=kx+b\; \; \Rightarrow \quad \left \{ {{2=1\cdot k+b} \atop {4=3\cdot k+b}} \right.\; \; \left \{ {{b=2-k} \atop {4=3k+(2-k)}} \right.\; \left \{ {{b=2-k} \atop {2k=}2} \right. \; \left \{ {{b=1} \atop {k=1}} \right. \; \; \Rightarrow \\\\\underline {EF:\; \; y=x+1}\; \; \; \Rightarrow \quad k_{EF}=1$

Найдём координаты середины отрезка EF - точки М .

$x_{M}=\frac{x_{E}+x_{F}}{2}=\frac{1+3}{2}=2\; \; ,\; \; y_{M}=\frac{y_{E}+y_{F}}{2}=\frac{2+4}{2}=3\\\\M(2,3)$

Составим уравнение серединного перпендикуляра МН. Так как МН⊥EF , то их угловые коэффициенты связаны соотношением

$k_{EF}\cdot k_{MH}=-1\; \; \to \; \; \; k_{MH}=-\frac{1}{k_{EF}}=-\frac{1}{1}=-1\; \; .$

Составим уравнение МН , подставляя в уравнение прямой у=kx+b значения k=-1 b и координаты точки М: x=2 , y=3 :

$3=-1\cdot 2+b\; \; \to \; \; b=5\; \; \; \Rightarrow \\\\\underline {MH:\; \; y=-x+5}$

Точка пересечения серединного перпендикуляра МН и оси ОУ ( х=0 ) будет искомой точкой, которая равноудалена от точек E и F и лежит на оси ОУ.

$\left \{ {{y=-x+5} \atop {x=0}} \right. \; \; \Rightarrow \; \; \left \{ {{y=5} \atop {x=0}} \right. \; \; \Rightarrow \; \; H(0,5)$

** оси ординат Найдите точку равноудаленную от точек е(1;2) f (3;4)​

** оси ординат Найдите точку равноудаленную от точек е(1;2) f (3;4)