Ответ:
Чертежи см. на рисунке.
Объяснение:
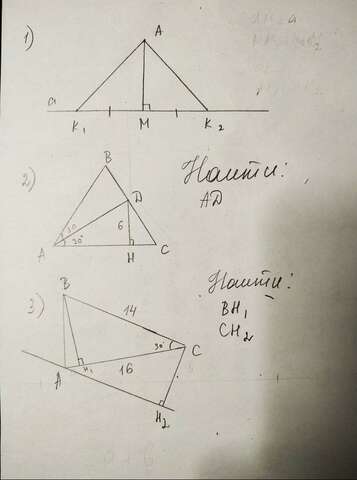
Задача №1
1) Так как K₁ и K₂ принадлежат прямой а, то отрезок K₁K₂ принадлежит прямой а.
2) Рассмотрим ΔK₁AK₂:
Так как АМ⊥K₁K₂ и МK₁ = МK₂, то АМ-высота и медиана ⇒ ΔK₁AK₂-равнобедренный. Отсюда следует, что AK₁=АK₂. Ч.Т.Д
Задача №2
1) Так как ΔАВС-равносторонний, то ∠А=60°. Значит ∠DAH=30°(АD-биссектриса)
2) Рассмотрим ΔАDН:
∠АНD=90°
∠DAH=30°,
значит DH=1/2АD - катет, лежащий напротив угла в 30°.
Отсюда АD=2*DH=2*6=12см
Ответ: 12см
Задача №3
1) Т.к. ВС||АН₂, АС-секущая, то ∠ВСА=∠САН₂=30° как накрест лежащие
2) Рассмотрим ΔАСН₂:
∠САН₂=30°
∠АН₂С=90° (расстояние=перпендикуляр)
значит СН₂=1/2АС - катет, лежащий напротив угла в 30°.
Отсюда СН₂=1/2*16=8см
3) Рассмотрим ΔВСН₁:
∠ВСН₁=30°
∠ВН₁С=90° (расстояние=перпендикуляр)
значит ВН₁=1/2ВС - катет, лежащий напротив угла в 30°.
Отсюда ВН₁=1/2*14=7см
Ответ: ВН₁=7см; СН₂=8см