Ответ: arcsin 0,99846, что соответствует углу 86,82°
Объяснение:
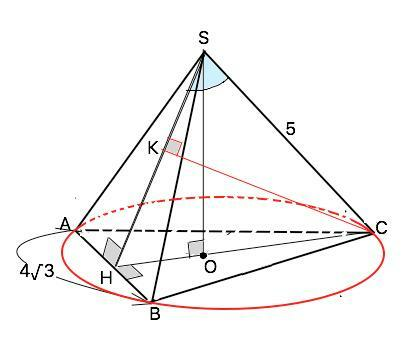
Основание правильной пирамиды – правильный многоугольник, боковые грани - равнобедренные треугольники, а вершина проецируется в центр окружности, описанной около основания.
Рассмотрим рисунок приложения:
Для правильного треугольника R=a/√3, где а- сторона основания. ОС=R=4√3:√3=4. Из отношению катета и гипотенузы ОС:SС=4:5 следует ∆ SОС - египетский, ⇒ высота пирамиды SО=3
Проведем высоту СН основания и апофему грани SAB. Высота СН⊥АВ. По т. о 3-х перпендикулярах SН⊥АВ.
SН и СН лежат в плоскости SСН. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости. ⇒ АВ перпендикулярна плоскости SСН. ⇒ Плоскость SСН⊥АВ.
Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.⇒ (SСН)⊥(АSВ). ⇒
Искомый угол СSН
* * *
Способ 1) СН=АС•sin60°=4√3•√3/2=6 ⇒
2S(СSН)=SО•СН=3•6=18.
НО=СН-СО=6-4=2.
SН=√(SО²+ОН²)=√(9+4)=√13
Проведем высоту СК к стороне SН.
2S(CSH)=СК•SН ⇒ CK=2S:SH=18/√13 Синус СSК=СК:СS= (18/√13):5=0,99846, что соответствует углу 86,82°
Способ 2): Вычислить нужный угол можно с тем же результатом по т. косинусов: СН²=SН²+СS²-2•SН•SС•cos(CSH) .