Боковая сторона равнобедренного треугольника точкой касания вписанной окружности делится...

Question

Боковая сторона равнобедренного треугольника точкой касания вписанной окружности делится в отношении 12:5 считая от вершины угла при основании треугольника. найдите радиус вписанной окружности если площадь треугольника равняется 1680 см^2

Answer 1

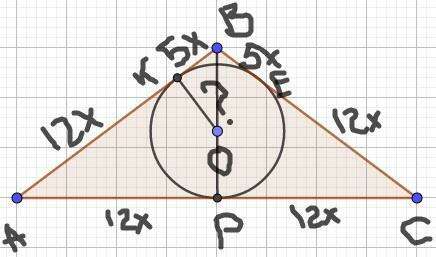
S = pr, где p = 0,5(AB + BC + AC) = 0,5(17x + 17x + 24x) = 29x.  

По формуле Герона S =√(p(p - AB)(p - BC)(p - AC)) =  

=√(29x(29x - 17x)(29x - 17x)(29x - 24x)) = √(29x∙12x∙12x∙5x) = 12√(145)x².

Имеем, 12√(145)x² = 1680; √(145)x² = 140; x² = 140/√(145) = 140√(145)/145 =

= 28√(145)/29; x = √(28√(145)/29) = 2√(7√(145)/29).

p = 29∙2√(7√(145)/29) = 2√(29∙7√(145)) = 2√(203√(145))  (см).

r = S/p = 1680/2√(203√(145)) = 840/√(203√(145))(см).

---