Ответ: 166 2/3 см³
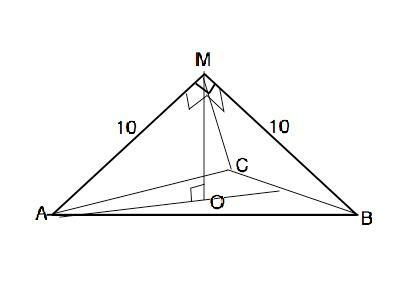
Объяснение: Формула объёма пирамиды V=S•h/3. Назовём пирамиду МАВС. Все боковые ребра правильной пирамиды равны. МА=МВ=МС=10 см Т.к. углы боковых граней при вершине М=90°, углы при основаниях боковых граней равны по 45°, а их основания равны 10:sin45°=10√2. Вершина правильной пирамиды проецируется в центр описанной около основания окружности. Её радиус ОА=АВ/√3=10√2:√3. Высота пирамиды перпендикулярна основанию, ∆ АМО прямоугольный. По т.Пифагора высота МО=√(AM*-AO*)=√[10*-(10√2:√3)*]=10/√3
S=AB²√3/4=(10√2)²•√3/4=200√3/4
V=((200√3/4)•10/√3):3=500/3=166 2/3 см³