95 баллов.... Решите пожалуйста

Question

Дан 1 ответ

2ReCKey_zn · Answer 1 · 2020-06-03T14:33:39+0000

1)

$sin(2x)+cos(2x)=2tg(x)+1\\2sin(x)cos(x)+1-2sin^2(x)=2tg(x)+1\\2sin(x)cos(x)-2sin^2(x)=2tg(x)\\2sin(x)(cos(x)-sin(x))=2tg(x)\\cos(x)-sin(x)=\frac{1}{cos(x)}\\ cos^2(x)-sin(x)cos(x)=1\\2cos^2(x)-2sin(x)cos(x)=2\\2cos^2(x)-1+1-sin(2x)=2\\cos(2x)-sin(2x)=1$

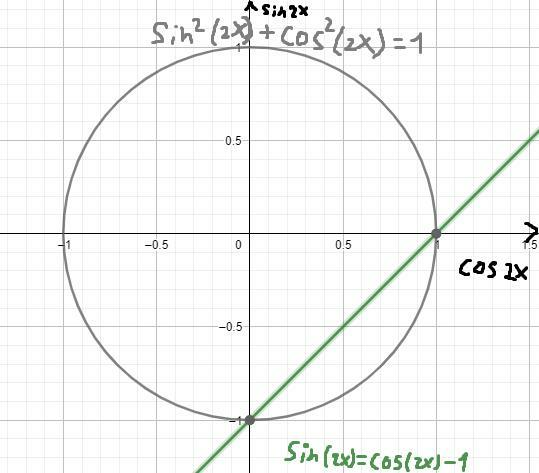
На данной стадии можно уравнение решить графически, нарисовав график прямой и тригонометрической окружности, в координатах sin(2x) и cos(2x) (см. рисунок) и потом решить 2 уравнения: cos(2x)=1 и sin(2x)=(-1)

Или ввести вспомогательный аргумент, что я и сделаю.

$cos(2x)-sin(2x)=1\\\sqrt{2}(\frac{1}{\sqrt{2}} cos(2x)-\frac{1}{\sqrt{2}}sin(2x))=1\\ sin(\frac{\pi}{4}-2x)=\frac{1}{\sqrt{2}}\\\frac{\pi}{4}-2x_1=\frac{\pi}{4}+2\pi k\\x_1=-\pi k\\\frac{\pi}{4}-2x_2=\frac{3\pi}{4}+2\pi k\\-2x_2=\frac{\pi}{2}+2\pi k\\ x_2=-\pi k-\frac{\pi}{4}$

--------------------

2)

$4sin^2(x)+3tg^2(x)=1\\4sin^2(x)cos^2(x)+3sin^2(x)=cos^2(x)\\sin^2(2x)=cos^2(x)-sin^2(x)-2sin^2(x)\\sin^2(2x)-cos(2x)=1-2sin^2(x)-1\\1-cos^2(2x)-2cos(2x)=-1\\cos^2(2x)+2cos(2x)-2=0\\cos(2x)=a\\a^2+2a-2=0\\\frac{D}{4}=1+2=3\\ a_1=\sqrt{3}-1\\ a_2=-\sqrt{3}-1$

так как 2 корень меньше -1 он нам не подходит.

$cos(2x)=\sqrt{3}-1\\2x=(+-)arccos(\sqrt{3}-1)+2\pi k\\x=(+-)\frac{1}{2}arccos(\sqrt{3}-1)+\pi k$

--------------------

3)

$4sin(x)sin(2x)sin(3x)=sin(4x)$

тут сразу напрашивается формула произведение синусов в разность косинусов.

$2sin(x)*(cos(x)-cos(5x))=sin(4x)\\sin(2x)-2sin(x)cos(5x)=sin(4x)\\sin(2x)-sin(4x)=2sin(x)cos(5x)\\sin(2x)-sin(4x)=sin(6x)-sin(4x)\\sin(2x)=sin(6x)\\2x_1=arcsin(sin(6x_1))+2\pi k\\2x_1=6x_1+2\pi k\\x_1=-\frac{pi}{2}k\\2x_2=\pi-6x_2+2\pi k\\8x_2=\pi (1+2k)\\x_2=\frac{\pi}{8}(1+2k)$

---------------

Ты эти задачи с какой-то олимпиады понабирал?

Если тебе такое дз дали, то не повезло тебе.

2ReCKey_zn (356 баллов) 03 Июнь, 20

95 баллов.... Решите пожалуйста​

95 баллов.... Решите пожалуйста