1. Трапеция АВСД (АД и ВС- основания) расположена вне плоскости альфа. Диагонали трапеции...

Question

1. Трапеция АВСД (АД и ВС- основания) расположена вне плоскости альфа. Диагонали трапеции параллельны плоскости. Через вершины А и В проведены параллельные прямые, которые пересекают плоскость альфа в точках Е и Ф соответственно. Докажите, что ЕАВФ- параллелограмм. Постройте рисунок
2. На рисунке 1 плоскости альфа и бета параллельны. Прямая а пересекает плоскости альфа и бета соответственно в точках А и В, а прямая б- в точках С и Д. Каково взаимное положение прямых а и б? Поясните.
3. Дан параллелипипед АВСДА1В1С1Д1, все грани которого- прямоугольники , АД=4, ДС=8, СС1=6. Постройте сечение параллелипипеда плоскостью, проходящей через середину ребра ДС и параллельной плоскости АВ1С1, и найдите периметр сечения.

Answer 1

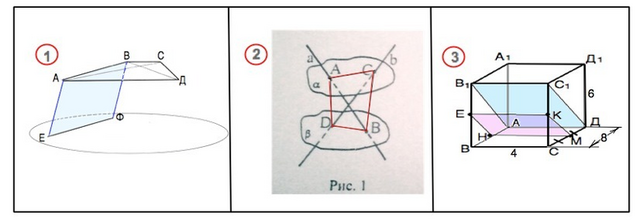
1) 

Диагонали трапеции - пересекаются . Поскольку они параллельны плоскости α, следовательно,  плоскость, в которой они лежат, параллельна плоскости α, и все стороны трапеции также параллельны плоскости α. 

Параллельные прямые ЕА и ВФ задают плоскость. Если две параллельные плоскости пересечены третьей, то  линии  их пересечения параллельны.  ⇒ АВ||ЕФ, АЕ||ВФ по условию ⇒ в четырехугольнике АВФЕ противоположные стороны параллельны. АВФЕ - параллелограмм. 

2) 

Данная без нужного рисунка задача вполне может остаться без решения. 

Прямые, пересекающие параллельные плоскости, могут:  

пересекаться, быть параллельными или скрещивающимися. 

Через две параллельные или  через две пересекающиеся прямые, можно провести плоскость, притом только одну.  

 Если две параллельные плоскости   (α и β )  пересечены третьей, то линии их пересечения параллельны. И тогда на рисунке в любой проекции они будут параллельны (или совпадут). На данном рисунке АС и DB не параллельны. Следовательно, точки А, С, В и Д не лежат в одной плоскости, а прямые a и b не пересекаются и не параллельны. Они - скрещивающиеся. 

3)

Так как все грани параллелепипеда прямоугольники, наклонные В1А и С1Д  перпендикулярны АД, и  АДС1В1 - прямоугольник. 

Пусть точка М - середина СД. 

Проведем МК║ДС1, МН║АД и КЕ║||В1С1. 

НМ=КЕ ( параллельны и равны равным сторонам равных граней). КМ=КН, параллельны диагоналям параллельных граней и делят ребра СС1 и ВВ1 пополам.  

В прямоугольном треугольнике КСМ  стороны СМ=8:2=4, КС=6:2=3, треугольник КСМ - египетский и КМ=5

Периметр - сумма длин всех сторон многоугольника. 

Р сечения =2•(НМ+КМ)=2•(4+5)=18 (ед. длины)

---