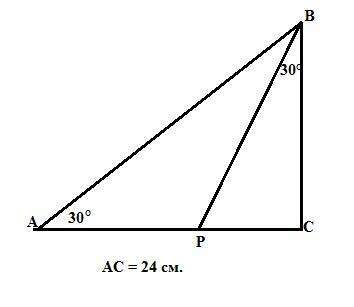
Ответ:
ВР= 16 см.
Объяснение:
Катет, лежащий против угла 30°, равен половине гипотенузы.
Пусть катет ВС = х, тогда гипотенуза АВ = 2х и по Пифагору
АВ² - ВС² = АС² или 3х² = 24². => х = 8√3 см.
Проведем биссектрису угла В, равного 60° (по сумме острых углов прямоугольного треугольника РВС. Тогда ∠СВР = 30°
Пусть в треугольнике РВС катет РС = х (лежит против угла 30°). Гипотенуза ВР = 2х и по Пифагору 3х² = (8√3)². => х = 8 см..
Тогда ВР = 2х = 16см.