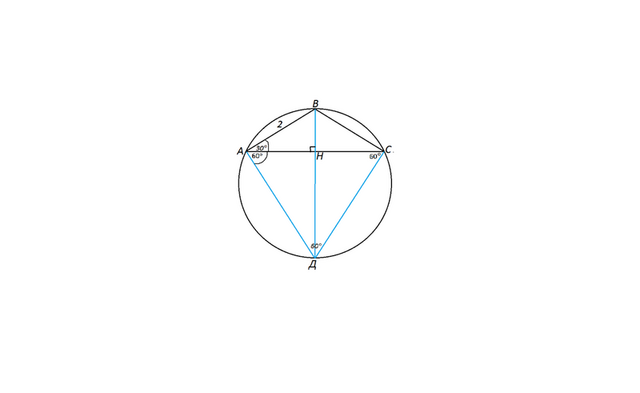
Сделаем рисунок к задаче.
Треугольник АВС - тупоугольный,
центр описанной окружности находится вне его.
Углы при основании АС равнобедренного треугольника с углом при вершине, равным 120° равны (180°-120°):2=30°.
Проведем диаметр ВД как продолжение высоты треугольника АВС.
Соединим А и С с точкой Д пересечения диаметра и окружности.
Углы ВАД и ВСД прямые - опираются на диаметр.
Углы САД и АСД равны 60° (90°-30°=60°.
Можно также вспомнить, что сумма противоположных углов вписанного четырехугольника равна 180 °, а четырехугольник АВСД безусловно вписанный, поэтому угол АДС=60°.)
Треугольник АДС - равносторонний - все его углы равны 60°,
следовательно, все стороны равны.
В треугольнике АВН сторона АН=АВ*cos(30)=√3 отсюда АС=АД=СД=2√3
ДН=АС*sin(60)=(2√3)*√3):2=3 см
Диаметр описанной окружности равен сумме высот треугольников
АВС и АСД.
Высота ВН как противолежащая углу 30° равна половине АВ=1 см
Диаметр ВД=3+1=4 см
---------------
Более короткое решение -
Найдя величину угла АДС=60°, найдем величину угла АДВ=30°.
АВ противолежит углу АДВ, равному 30°, и потому равна половине диаметра ВД.
Отсюда ВД=2*2=4 см