8 клас, тригонометрические функции Найдите диагональ ромба со стороной 6 см. и острым...

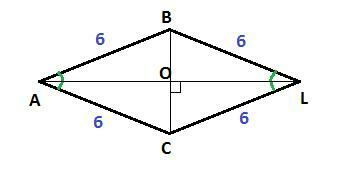
Дано : ромб ABLC , AB=BL=LC=AC=6 см, ∠CLB = ∠L

Найти : AL, BC

Решение :

Диагонали ромба пересекаются под прямым углом, точкой пересечения делятся пополам, являются биссектрисами углов ромба и делят ромб на 4 равных прямоугольных треугольника.

Рассмотрим ΔСLO; CL = 6 см - гипотенуза, ∠CLO=∠L/2

Отношения в прямоугольном треугольнике

$\sin\angle CLO=\dfrac{CO}{CL}\\\\CO=CL\cdot \sin\angle CLO\ \ \ \Rightarrow\ \ \ CO=6\sin\dfrac{\angle L}2\\\\\cos\angle CLO=\dfrac{LO}{CL}\\\\LO=CL\cdot \cos\angle CLO\ \ \ \Rightarrow\ \ \ LO=6\cos\dfrac{\angle L}2$

Диагонали вдвое больше найденных катетов

$BC=2\cdot 6\sin\dfrac{\angle L}2\boldsymbol{=12\sin\dfrac{\angle L}2}$ см

$AL=2\cdot 6\cos\dfrac{\angle L}2\boldsymbol{=12\cos\dfrac{\angle L}2}$ см