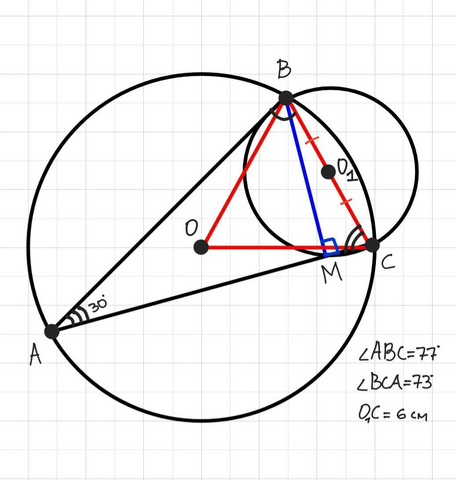
Дано: ΔАВС, ∠В= 77°, ∠С= 73°, ВМ – высота, ВМ⟂АС, т.О – центр окружности, опис. около ΔАВС, т.О1 – центр окружности, опис. около ΔBMC, R1=OC1= 6 см.
Найти: ОВ.
Решение.
1) Рассмотрим ΔВМС. По условию он прямоугольный (поскольку ВМ⟂АС), а это значит, что диаметр окружности, описанной около этого треугольника, будет равен гипотенузе. Т.е. d=BC, а отрезки ВО1 и О1С являются радиусами.
ВО1=О1С= 6 см.
А диаметр ВС= 2•ВО1= 2•6= 12 см.
2) Найдем ∠А.
Сумма углов треугольника равна 180°, значит, в ΔАВС:
∠А= 180°–∠В–∠С= 180°–77°–73°= 30°.
3) ∠А=30° => данный угол является вписанным в окружность с центром О.
А ∠ВОС — центральный угол окружности с центром О. При чем углы ∠А и ∠ВОС опираются на одну и ту же дугу.
4) Вспоминаем свойство: вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
Значит, ∠А= ½∠ВОС => ∠ВОС= 2∠А.
∠ВОС= 2•30°= 60°.
5) Центральный угол ВОС равен 60°. Треугольник ВОС равнобедренный, ОВ=ОС (радиусы), угол при вершине 60° => ΔВОС равносторонний.
Поскольку ВОС – равносторонний треугольник, то ОВ=ОС=ВС= 12 см.
Радиус окружности, описанной около треугольника ABC равен 12 см.
Ответ: 12 см.