В треугольнике АВС , угол С равен 90 ,проведена биссектриса СD. Угол BDC =105 , АС=6 см....

Question

В треугольнике АВС , угол С равен 90 ,проведена биссектриса СD. Угол BDC =105 , АС=6 см. Найдите угол А, сторону АВ.

Answer 1

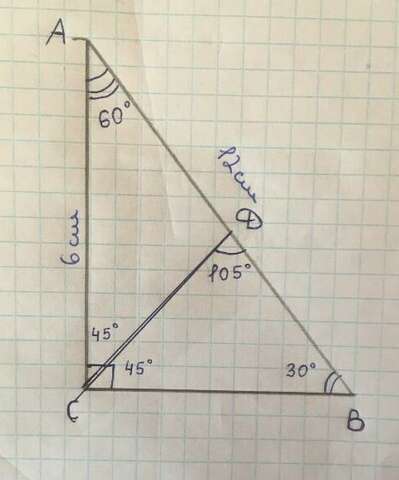
Дано:

△ABC - прямоугольный

∠C = 90˚

CD - биссектриса ∠ACB

∠BDC = 105˚

AC = 6 см.

Найти:

∠A; AB.

Решение.

Т.к. CD - биссектриса => ∠DCB = ∠ACD = 90 : 2 = 45˚

СУММА УГЛОВ ТРЕУГОЛЬНИКА РАВНЯЕТСЯ 180°

=> ∠B = 180 - (45 + 105) = 30˚

Если острый угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.

=> AB = 6 * 2 = 12 см.

СУММА ОСТРЫХ УГЛОВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВНЯЕТСЯ 90°.

=> ∠A = 90 - 30 = 60˚

Ответ: 12 см; 60°.

---