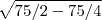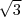Задание 1:(по шагово)
1.Окружность состоит из 360 градусов, хорда стягивающая дугу в
120 градусов стягивает треть окружности (360/120=3). Следовательно
75пи/3=25пи.
2. Проведем из центра окружности 2 радиуса к концам хорды. Получим
равнобедренный треугольник с углом у центра окружности в 120 градусов, и
углами у основания - по 30 градусов (120+30+30=180).
Найдем длину радиуса окружности 2пиR=75пи, R=75/2
Проведем высоту из центра окружности к хорде (основанию
равнобедренного треугольника), получим два равных прямоугольных
треугольника с известными углами (90, 60, 30 гадусов) и известной
гипотенузой (равной длине радиуса). Ищем сначала длину катета (высоты к
хорде) против угла в 30 градусов (равен половине гипотенузы), т.е. 75/4,
затем по теореме пифагора находим длину вторго катета, равного 1/2
хорды(вниу 1 фотография) Получаем 5(внизу вторая фотка, просто пишешь сюда зачок кос и 3)/2. Следовательно вся хорда будет в два раза длинее, т.е. 5(2 фотка, значок кос 3)
Заданее 2:
Нам дана окружность № 1, радиус ее 12 см. Найдем длину окружности № 1:
L1 = 2П(R1) = 2П12 = 24П.
Эту окружность разогнули в дугу с центральным углом в 135 градусов.
То есть, если эту дугу дорисовать до окружности, то получится новая
окружность № 2. Чтобы найти радиус этой новой окружности найдем длину
дуги окружности, которая приходится на один градус этой окружности № 2 и
умножим на 360 градусов. Получаем длину окружности № 2:
L 2 = (24П/135) * 360 = 64П.
Теперь мы знаем длину окружности № 2 и знаем формулу длины окружности, следовательно можем найти радиус окружности № 2.
L 2 = 2П (R2);
R2 = (L 2) / 2П;
R2 = 64П / 2П = 32 ед.
Рассмотрим треугольник в окружности № 2, образованный радиусами и хордой, стягиваемой дугой.
По теореме косинусов имеем:
(хорда2)^2 = (радиус)^2 + (радиус)^2 - 2*радиус*радиус*Cos(135);
(хорда2) = корень из [2*радиус^2 - 2*радиус^2*Cos(3П/4)];
(хорда2) = корень из [2*радиус^2 *(1- Cos(3П/4)];
(хорда2) = корень из [2*32^2 *(1+ [корень из 2] / 2)];
хорда2 = 32 корень из (2 + корень из 2).