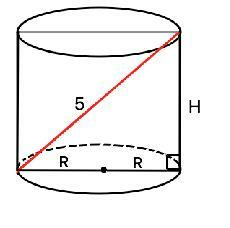
Площадь боковой поверхности цилиндра больше площади его основания в 3 раза. Найдите площадь полной поверхности цилиндра, если диагональ его осевого сечения равна 5 см.
————
Формула площади боковой поверхности цилиндра S(б)=H•2πR, где Н - высота цилиндра, R- радиус основания.
Формула площади основания цилиндра ( круга) S(о)=πR²
По условию H•2πR=3πR².
Из этого отношения выводим 2Н=3R и Н=1,5 R.
Осевое сечения цилиндра - прямоугольник. Диагональ делит его на два равных прямоугольных треугольника.
Здесь диагональ D = гипотенуза=5 см, катеты Н=1,5R, и d=2R.
По т.Пифагора D²=(1,5H)²+(2R)²
25=6,25R² ⇒ R=2 см, Н=1,5•2=3 см
S(полн)=Ѕ(бок)+2•Ѕ(осн)
Ѕ(полн)=3•4π+2˙π•2²=20π см²