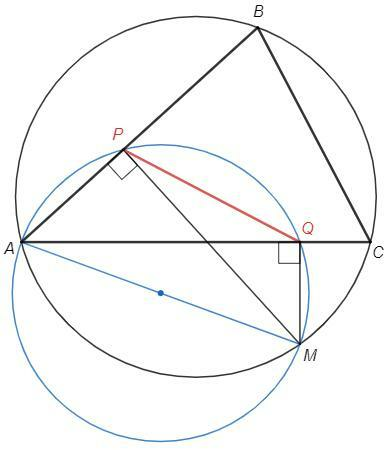
Углы APM и AQM - прямые.
Отрезок AM виден из точек P и Q под прямым углом - точки P и Q лежат на окружности с диаметром AM.
Окружность с диаметром AM - описанная окружность △APQ.
Теорема синусов
PQ/sin(PAQ) =2R =AM
Угол A не меняется, следовательно длина PQ зависит от длины AM.
Отрезок AM - хорда в описанной окружности △ABC.
Максимальная хорда - диаметр.