Объяснение:
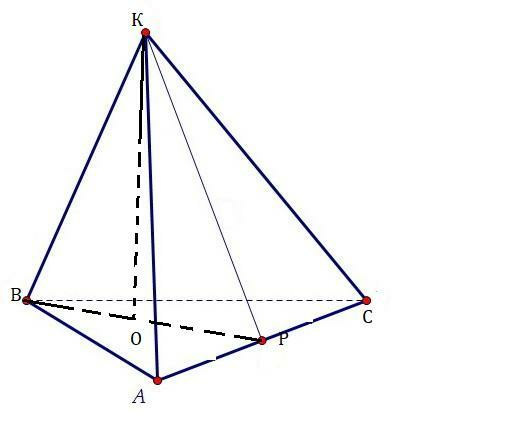
Пирамида КАВС, КО-высота пирамиды. В основании лежит ΔАВС, АВ=ВС, АС=30, ВК⊥АС, ВК=36.
V=1/3 S(осн)*H. S(осн)=1/2*АС*ВР, S(осн)=1/2*30*36=540 (см²).
Т.к. ВР⊥АС, то и КР⊥АС по т. о трех перпендикулярах. Значит ∠КРО=45° , как линейный угол между плоскостью основания и боковой гранью. ВО/ОР=2/1 , ОР=12 .
ΔКОР-прямоугольный и равнобедренный т.к. ∠ОКР=90°-45°=45°. Значит ОР=ОК=12.
V=1/3 *540*12=2160 (см³).