Помогите с решением!

$1) 3^x = 4 - x$

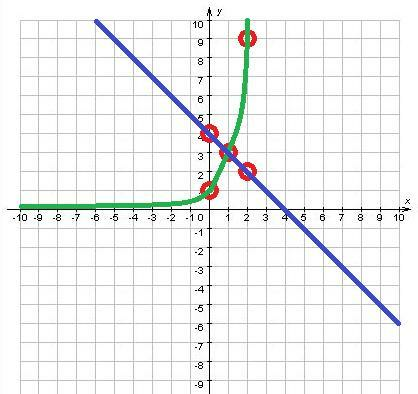
Данное уравнение можно решить графически, нарисовав графики функций $y = 3^x$ (показательная) и $y = 4 - x$ (прямая). Там где графики пересекутся - там и будет решение этого уравнения.

Как мы видим из графика, координатой точки пересечения функций является точка $(1;3)$ .

Ответ к уравнению №1: $x = 1$

$2) 5^x + 4 = 5^{2x} \cdot 5\\\\5\cdot5^{2x} - 5^x - 4 = 0\\\\5^x= z\\\\5z^2 -z - 4 = 0\\\\D = 1 + 80 = 81\\\\\sqrt D = 9\\\\z_1 = \frac{1-9}{10} = -0,8\\\\z_2 = \frac{1+9}{10} = 1\\\\5^x = -0,8$

Решения на множестве действительных чисел $R$ не возможно.

$5^x = 1\\\\5^x = 5^0\\\\x=0$

Ответ к уравнению №2: $x = 0$

$3) sin2x - sinx = 0\\\\2sinxcosx - sinx = 0\\\\sinx(2cosx - 1) = 0\\\\sinx=0\\\\x_1 = \pi n, n \in Z\\\\2cosx - 1 = 0\\\\2cosx = 1\\\\cos x = \frac{1}{2}\\\\x_2 = \frac{\pi}{3} + 2\pi n, n\in Z$

Ответ к уравнению №3: $x_1 = \pi n, n \in Z$ ; $x_2 = \frac{\pi}{3} + 2\pi n, n \in Z$

$4) lg(x-8) = lg(2x-6)\\\\x - 8 = 2x - 6\\\\x-2x = -6 + 8\\\\-x = 2\\\\x = -2$

Ответ к уравнению №4: $x = -2$