Ответ:
2,0096 cм²
Пошаговое объяснение:
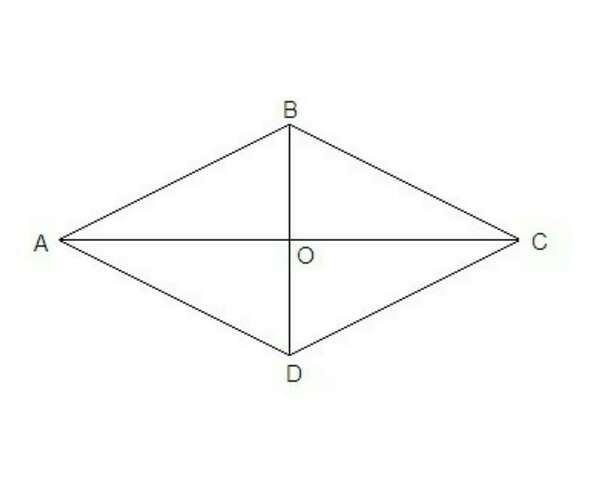
Диагонали ромба взаимно перпендикулярны и делятся точкой пересечения пополам.
АО = 3 см, ВО = 4 см.
Из прямоугольного треугольника АОВ по теореме Пифагора:
АВ = √(АО² + ВО²) = √(3² + 4²) = √(9+16) = √25 = 5 см
Для любого многоугольника, в который можно вписать окружность, справедлива формула:
S = pr, где р - полупериметр.
р = 15 · 4 / 2 = 30 см
Sabcd = АС · BD / 2 = 6 · 8 / 2 = 24см²
r = S / p = 24/30 = 0,8 см
Sкруга = πr² = 2,0096 cм²(приблизительно)