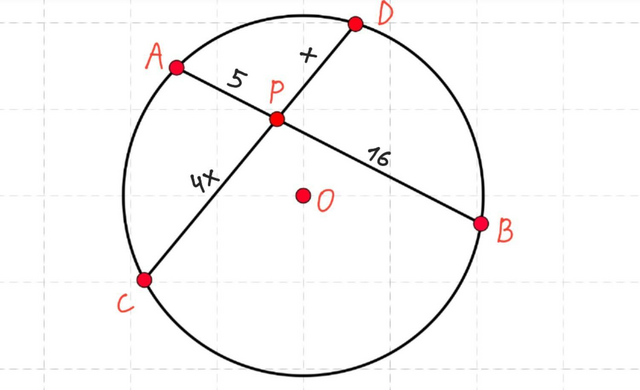
Дано: окружность, О - центр, AB и CD — хорды, AB∩CD= т.Р, АР= 5, ВР= 16, DP= 4CP.
Найти: СР.
Решение.
По условию СР в 4 раза больше DP. Пусть DP= x, тогда CP= 4x.
Согласно теореме о пересекающихся хордах окружности, если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Таким образом, получаем равенство:
AP•BP= CP•DP;
5•16= 4x•x;
80= 4x²;
x²= 20;
x= √20= 2√5 (е.д.)
РС= 4х= 4•2√5= 8√5 (е.д.).
Ответ: 8√5 е.д.