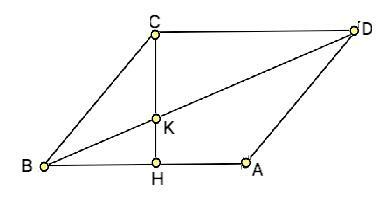
Вариант решения.
Ответ: 10 (ед. длины)
Объяснение:
Одна из формул площади параллелограмма
S=a•b•sinα, где а и b стороны с общей вершиной, α - угол между ними.
Ромб - параллелограмм с равными сторонами.
S=a•a•0.8=320 ⇒ a²=320:0,8=400 ⇒ a=√400=20. ⇒ АВ=ВС=20
Опустим высоту СН. Из ∆ СВН высота ромба СН=СВ•sinB=20•0,8=16
По т.Пифагора ВН=√(BC²-CH²)=12
Примем длину СК=х. Тогда КН=16-х.
Прямоугольные треугольники ВКН и СКD подобны по равному острому углу при К. Из подобия следует отношение:
СD:BH=CK:KH
20:12=x:(16-x)
Решив уравнение, получим х=10.
СК=10 ( ед. длины)