Решить неравенство:

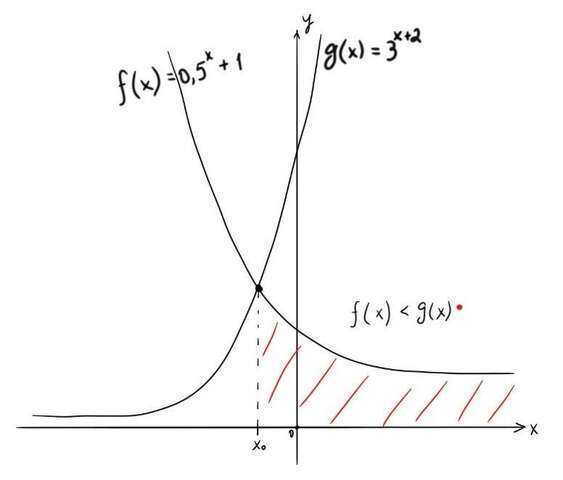
Более альтернативного решения не видно, поэтому применяем подбор предварительно начертив приблизительный график обеих функций.

$f(x) = 0.5 {}^{x} + 1 = {2}^{ - x} + 1 \\ E(f): \: {2}^{ - x} \in ( - \infty ;0) \\ {2}^{ - x} + 1 \in ( - \infty ;1) \rightarrow f \in ( - \infty ;1)$

$g(x) = {3}^{x + 2} = 9 \times {3}^{x} \\ E(f): \: {3}^{x} \in (0;\infty) \\ 9 \times {3}^{x} \in (0;\infty) \rightarrow g \in ( 0;\infty)$

На графике видно, что пересечение функций одно (корень х₀) и решением будет все числа по правой части от корня. Осталось найти корень, но данное неравенство не решить обычными методами, поэтому пробуем подбор:

$x = 0 \\ 0.5 {}^{0} + 1 = {3}^{0 + 2} \\ 2≠ 9 \rightarrow x≠ 0 \\ x = - 1 \\ 0.5 {}^{ - 1} + 1 = {3}^{ - 1 + 2} \\ 2 + 1 = 3 \\ 3 = 3 \rightarrow x = - 1$

Корень найден, хоть и не самым лучшим методом. Можно писать ответ:

$x \in ( - 1; + \infty )$