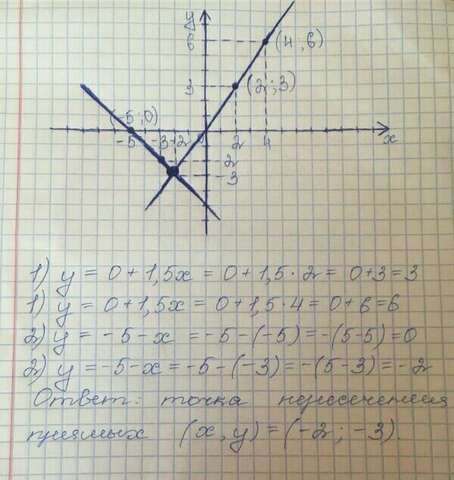
Решение:
Чтобы найти точку пересечения данной системы уравнений нужно перенести все члены каждого из уравнений в правую часть со сменой знака, а в левой части оставить переменную 
.
Теперь необходимо составить таблицу для переменных 
и , чтобы можно было подставлять значения выражений. После этого мы чертим координатную плоскость и находим точку пересечения прямых.
![1:\left[\begin{array}{ccc}x&y\\2&3\\4&6\end{array}\right] 2:\left[\begin{array}{ccc}x&y\\-5&0\\-3&-2\end{array}\right]](https://tex.z-dn.net/?f=1%3A%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7Dx%26y%5C%5C2%263%5C%5C4%266%5Cend%7Barray%7D%5Cright%5D%202%3A%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7Dx%26y%5C%5C-5%260%5C%5C-3%26-2%5Cend%7Barray%7D%5Cright%5D "1:\left[\begin{array}{ccc}x&y\\2&3\\4&6\end{array}\right] 2:\left[\begin{array}{ccc}x&y\\-5&0\\-3&-2\end{array}\right]")
График прикреплён. Точка пересечения указана внизу.
Ответ: 
