МОТОРНАЯ ЛОДКА ПРОШЛА 60 КМ ПО ТЕЧЕНИЮ РЕЧКИ И 36 КМ ПО ОЗЕРУ, ПОТРАТИВШИ НА ВЕСЬ ПУТЬ 5...

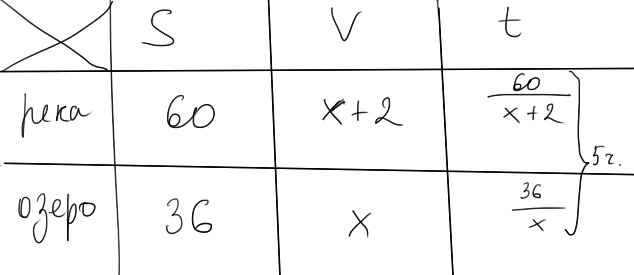
составим таблицу: (см ниже)

5 часов это общее время хождения лодки.

В озере нет течения, значит скорость обозначим за х

В реке лодка шла по течению значит скорость будет равна х + 2

составим уравнение:

$\frac{60}{x+2} + \frac{36}{x} = 5$

переносим в правую часть все числа и приравниваем к нулю:

$\frac{60}{x+2} + \frac{36}{x} - 5 = 0$

Найдем общий знаменатель:

$\frac{60x + 36(x+2) - 5x(x+2)}{x(x+2)}$

дробъ равна нулю, если числитель равен нулю, приравняем числитель к нулю:

60x + 36(x+2) - 5x(x+2) = 0

и решаем:

60x + 36x + 72 - 5x^2 - 10x = 0 (5x^2 - это 5x в квадрате)

-5x^2 + 86x + 72 = 0

D = 7396 - 4*(-5) * 72 = 7396 + 1440 =8836 => корень из 8836 = 94.

x(первое) = (-36 + 94) / -10 = 152/-10 = -15,2

х(второе) = (-36 - 94) / -10 = -130/-10 = 13

-15,2 - посторонний корень, т.к. скорость не может быть отрицательной.

13 - 2 = 11 - собственная скорость лодки.

вроде бы так хд

МОТОРНАЯ ЛОДКА ПРОШЛА 60 КМ ПО ТЕЧЕНИЮ РЕЧКИ И 36 КМ ПО ОЗЕРУ, ПОТРАТИВШИ ** ВЕСЬ ПУТЬ 5...