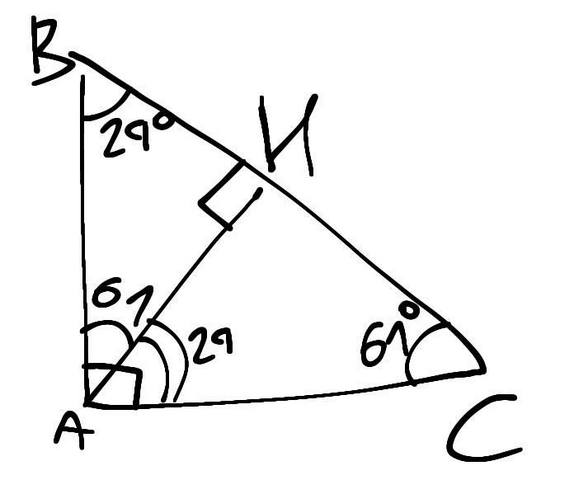
Высота, проведенная к гипотенузе, делит прямоугольный треугольник на два прямоугольных треугольника, каждые из которых подобен друг другу и искомому большому прямоугольному треугольнику.
Тоесть, ∆ABH ~ ∆AHC ~ ∆ABC
А как знаешь, у подобных треугольников соответственные углы равны.