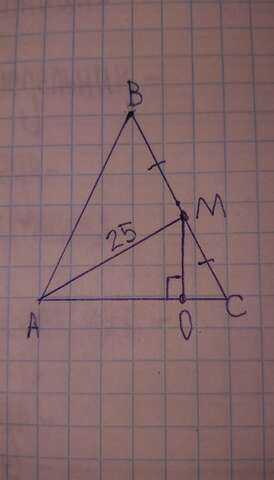Объяснение:
1. Угол MAC = 30°
Нам дан РАВНОСТОРОННИЙ треугольник, следовательно каждый его угол = 60°.
АМ в таком треугольнике будет являться и медианой, и высотой, и БИССЕКТРИСОЙ.
Если АМ биссектриса, значит она разделит угол ВАС пополам, сделовательно 60÷2 = 30°
2. Для начала разберёмся, что такое растояние от М до АС.
Растояние от М до АС это перпендикуляр, опущенный от М к АС (пусть этот отрезок будет МО).
У нас получается прямоугольный треугольник АМО.
АМ - гипотенуза, МО и АО - катеты.
Угол МАС мы нашли, он равен 30°.
Отсюда вытекает правило : катет, лежащий против угла в 30° равен половине гипотенузы.
Следовательно : МО = АМ ÷ 2 = 25 ÷ 2 = 12,5(см)