Ответ: 2,5
Объяснение: Основание правильной треугольной пирамиды - правильный треугольник, вершина высоты правильной пирамиды проецируется в центр основания.
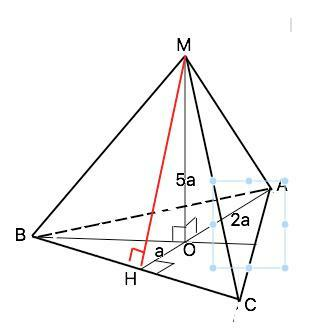
Назовем пирамиду МАВС, МО - высота пирамиды, АН - высота основания. Угол между плоскостью боковой грани и плоскостью основания - это угол МНА между апофемой МН и высотой АН основания, т.к. они перпендикулярны ребру угла между боковой гранью и основанием в одной точке Н.
Тангенсом является отношение катета, противолежащего углу, к прилежащему.
tgMHO=MO:OH. Примем коэффициент этого отношения равным а. Тогда ОН=а, МО=2а.
Центр правильного треугольника - точка пересечения его медиан ( высот, биссектрис) и делит их в отношении 2:1, считая от вершины. Поэтому ОА=2ОН=2а.
tgMAO=МО:АО=5a:2a=2,5.