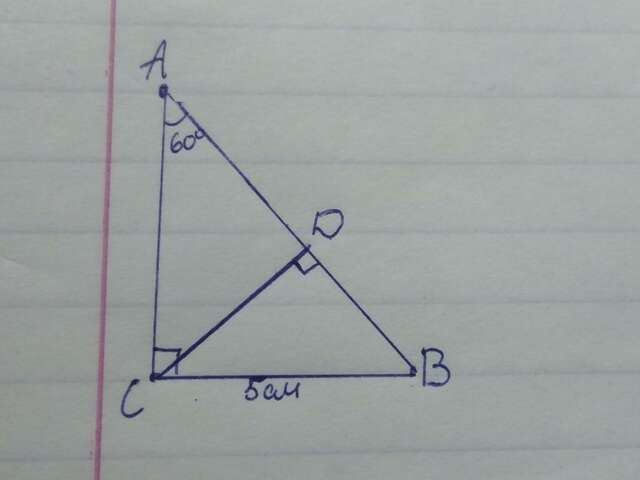
1. Высота CD — это перпендикуляр, проведенный из вершины к противолежащей стороне. Значит ∠ВDС = ∠CDA = 90°.
Зная это, мы можем найти ∠ACD.
∠ACD = ∠CDA −∠CAD = 90° − 60° = 30° (согласно 1-му свойству прямоугольных треугольников: «сумма двух острых углов прямоугольного треугольника равна 90°»)
2. Теперь узнаем, чему равен угол BCD и угол DBC:
∠BCD = ∠ACB −∠ACD = 90° − 30° = 60°
∠DBC = ∠ВDС −∠BCD = 90° − 60° = 30°
3. Теперь, зная чему равны все углы треугольника, мы можем найти длину высоты CD, применяя 2-е свойство прямоугольных треугольников: «катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы»
Т.к. в треугольнике CBD катет BC лежит перед прямым углом CDB, теперь он будет являться гипотенузой этого треугольника.
Значит, CD = ¹/₂BC
CD = 5 ÷ 2 = 2,5.
Ответ: ∠BCD = 60°; CD = 2,5 см.