Высота AM треугольника ABC делит его сторону BC на отрезки BM и MC.Найдите площадь...

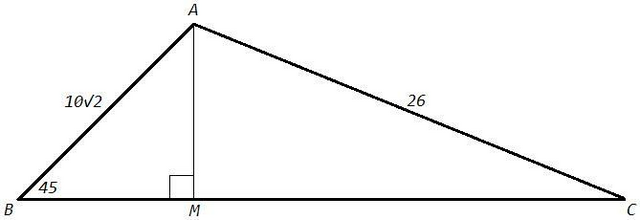
1) В треугольнике с углами 45, 90 (ABM) стороны относятся как 1:1:√2

AM=BM =AB/√2 =10

По теореме Пифагора (ACM)

MC =√(AC^2-AM^2) =24

S(ABC) =1/2 (BM+MC)*AM =1/2 *34*10 =170 (см^2)

2) AC/sinB =AB/sinC => sinC =10√2/26 *√2/2 =5/13

cosC =√(1 -sinC^2) =12/13

sinA =sin(B+C) =sinBcosC +cosBsinC =√2/2 (12/13 +5/13) =17√2/26

S(ABC) =1/2 AB*AC*sinA =1/2 10√2 *26 *17√2/26 =170 (см^2)

Высота AM треугольника ABC делит его сторону BC ** отрезки BM и MC.Найдите площадь...