1==============
Есть формула радиуса вписанной окружности по стороне:
r = (a√3)/6 = (12√3)/6 = 2√3
Есть другой вариант решения:
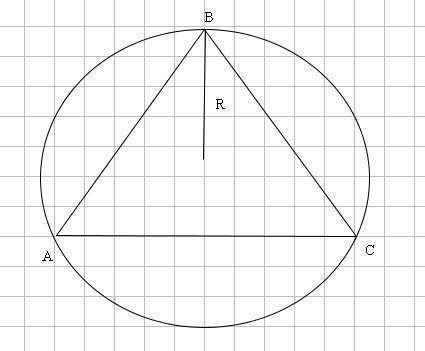
из формулы синусов, будем считать треуг. равнобедренный
при основании которого угол = 60 градусов, это равносторонний треугольник,
найдем радиус ОПИСАННОЙ окружности:
Используем формулу:
a=2r sin B = 2 r (√3/2) = √3 r
R = a/√3 = 12/√3
Но отношения радиусов описанной и вписанной окр. = 1/2
следовательно r = 1/2*(12/√3) = 6/√3
Результат тот же. Не верите ? проверьте :
(6/√3) *( √3/√3) =( 6√3)/3 = 2√3
2====================
Используем ту же формулу:
r = (a√3)/6
a√3 = 6r
a = 6r/(√3) = 12/√3 = ( 12/√3) *( √3/√3) = 4√3
3====================
Пока не знаю как решать
4====================
обозначим точки L и M на чертеже это точки серединн. перпенд.
Проведем анализ задания:
1 треугольники COL и BOL равны по двум сторонам
(OL - общая CL = LB по заданию) и углу между ними = 90 градусов
2 Аналогично: треугольники AOM и COM равны по
2м сторонам и углу между ними: (AM = MC по заданию, MO - общая, углы
OMC = OMA = 90 гр)
3 Если треугольники равны следовательно можем сделать выводы :
AO = OC
OC = OB
Следовательно AO = OB, отсюда следует, что треуг. AOB Равнобедренный.
Если мы найдем стороны AO мы найдем OC.
Рассмотрим треуг. AOB, он равнобедренный:
Найдем его углы, углы A и B равны.
угол A = угл B = (180 - 120)/2 = 30
Из теоремы синусов:
AO/sin B = AB/sin AOB
Найдем AO.
AO * sin AOB = AB * sin B
AO = (AB * sin B)/SIN AOB = (10 * SIN 30) / SIN 120 = (10 *1/2)/SIN 60 =
=5/(√3/2) = 10/√3
так как AO = OC что было доказано выше, следовательно
ОС =10/√3