Пусть R, r -- радиусы двух окружностей, O₁, O₂ -- их центры.
1. Взаимное расположение двух окружностей
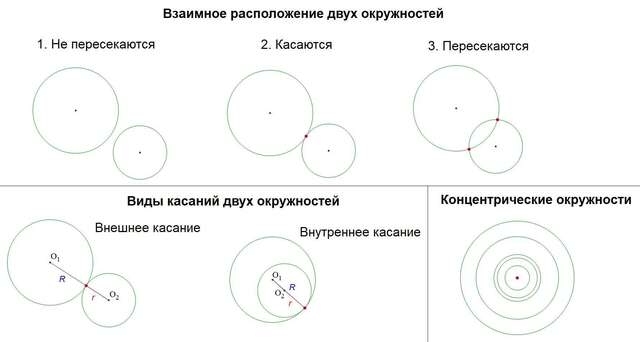
Выделяют три основных случая взаимного расположения окружностей:
- Две окружности не имеют общих точек (не пересекаются)
- Две окружности имеют одну общую точку (касаются)
- Две окружности имеют две общие точки (пересекаются)
Также выделяют иногда четвёртый случай: совпадающие окружности (бесконечное множество общих точек).
2. В каком случае окружности имеют одну общую точку?
Окружности будут иметь одну общую точку, если:
- Сумма их радиусов равна расстоянию между центрами (R + r = O₁O₂).
- Разность их радиусов равна расстоянию между центрами (R - r = O₁O₂).
3. Как называется общая точка двух окружностей?
Если окружности касаются в некоторой точке, то такая точка называется точкой касания.
Если пересекаются -- точкой пересечения.
4. Виды касаний двух окружностей
В пункте 2 было выделено два признака касания окружностей, откуда получается 2 вида касания:
- Внешнее касание (R + r = O₁O₂)
- Внутреннее касание (R - r = O₁O₂)
5. Когда окружности пересекаются?
Окружности пересекаются, когда расстояние между центрами меньше суммы радиусов, но больше их разности: R - r < O₁O₂ < R + r
6. Концентрические окружности
Окружности, имеющие общий центр, называются концентрическими.