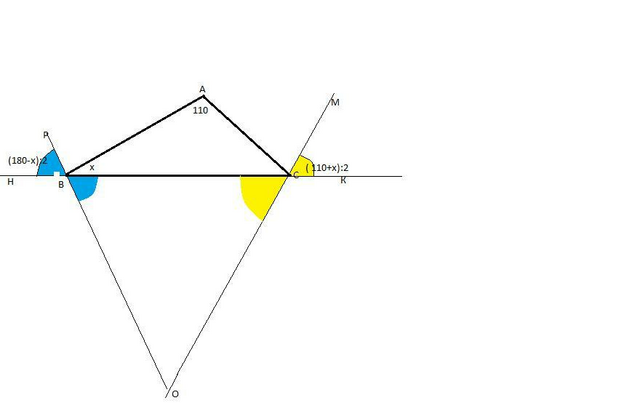
Прямые, содержащие биссектрисы внешних углов при вершинах В и С треугольника АВС, пересекаются в точке О.Найдите угол ВОС, если угол А равен 110 градусов.
Объяснение:
Пусть угол ∠АВС=х°, тогда для ΔАВС :
-внешний угол при вершине С, по т.о внешнем угле, равен ∠АСК=110°+х ,а ∠МСК=(110°+х) :2 , т.к СМ-биссектриса.
-весь внешний угол при вершине В равен (180°-х) , а его половина (180°-х):2.
Для ΔВОС : ∠В=∠РВН=(180°-х):2 как вертикальные;
∠С=∠МСК=(110°+х):2 как вертикальные.
По т. о сумме углов треугольника :
∠ВОС =180-(180°-х):2-(110°+х):2 или
∠ВОС =180-90°+х/2-55°-х/2 =35°
Ответ ∠ВОС=35°