Ответ:
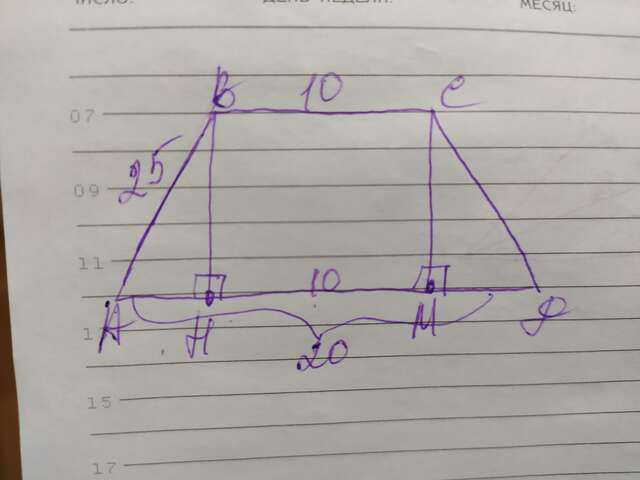
Объяснение: задание 7 (рисунок трапеции снизу)
Чтобы найти площадь трапеции по формуле (АД+АВ)÷2×h(h-высота трапеции, найдём высоту
Опустим с двух вершин верхнего основания для а нижнее две высоты: ВН и СМ. Они образуют на нижнем основании отрезок НМ=ВС=10см. Сумма отрезков АН + МД=20-10=10см. Так как трапеция равнобедренная, то АН=МД=10÷2=5см. Теперь рассмотрим полученный ∆АВН. Он прямоугольный. Зная 2 его стороны по теореме Пифагора найдём высоту ВН. ВН²=25²-5²=625-25=600; ВН=√600=√6×√100=10√6; ВН=10√6(см) Теперь, зная высоту, найдём площадь трапеции:
S=(10+20)÷2×10√6=30÷2×10√6=15×10√6=
=150√6. S=150√6(см). Так как нам нужно разделить площадь на √5, то:
150√6÷√5 (деление записывается дробью)
Задача 8
Площадь треугольника = сторона × высоту÷2. Нам для начала нужно найти основание, к которому проведена высота. Найдём по теореме Пифагора часть стороны получившегося прямоугольного треугольника:
17²-8²=289-64=225; сторона =√225=15. Сторона в прямоугольном треугольнике= половине основания 15(см), тогда полнак основаник треугольника= 15×2=30; основание=30(см). Теперь, найдём искомую площадь треугольника:
S=(30×8)÷2= 240÷2=120; S∆=120(cм)