Три окружности попарно касаются внешне. Радиус одной из них равен 6 см, а отрезок, соединяющий центры двух других равен 14 см. Найдите периметр треугольника, вершинами которого являются центры этих окружностей.
Ответ: 40 см
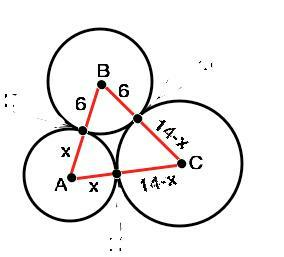
Объяснение: Нарисуем эти окружности Обозначим их центры А, В и С.(см. рисунок вложения).
Радиус одной окружности 6 см (дано).
Примем радиус второй окружности равным х см Тогда, поскольку сумма радиусов второй и третьей окружности равна 14 см, радиус третьей – 14-х. см
Периметр треугольника АВС=АВ+ВС+АС
АВ=6+х, ВС=6+14-х, АС=х+14-х.
Р= 6+х+20-х+14=40 (см)