У прямокутному трикутнику DBC(кут С=90 градусів) провели висоту СК. Знайдіть відрізок BK...

Question

У прямокутному трикутнику DBC(кут С=90 градусів) провели висоту СК. Знайдіть відрізок BK якщо DB=20см, ВС=10см​

Answer 1

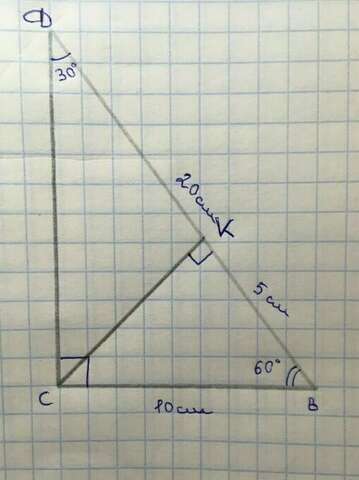
Дано:

△DBC - прямоугольный.

∠C = 90˚

CK - высота.

DB = 20 см.

BC = 10 см.

Решение.

ЕСЛИ КАТЕТ РАВЕН ПОЛОВИНЕ ГИПОТЕНУЗЫ, ТО НАПРОТИВ ЛЕЖАЩИЙ УГОЛ РАВЕН 30°

=> ∠D = 30˚

СУММА ОСТРЫХ УГЛОВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВНЯЕТСЯ 90°

=> ∠B = 90 - 30 = 60˚

△DCK и △BCK - прямоугольные т.к. CK - высота.

=> ∠KCB = 90 - 60 = 30˚

ЕСЛИ УГОЛ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВЕН 30°, ТО НАПРОТИВ ЛЕЖАЩИЙ КАТЕТ РАВЕН ПОЛОВИНЕ ГИПОТЕНУЗЫ.

=> BK = 10 : 2 = 5 см.

Ответ: 5 см.

---

Comments

Спасибо большое, можешь помочь еще 2 задачи пожайлуста